如何实现 Math.sqrt()

Math.sqrt() 即开平方根是很常用的一个计算方法，但具体是怎么实现的还真不了解，这篇文章就是叙述下这个方法具体是怎么计算的，并将平方根方法推广至求 N 次方根。

对于根号计算这种经常会产生无限不循环小数的操作，计算机的离散计算只能在一定精度的范围内进行逼近计算得到结果的近似值。

牛顿-拉弗森方法简介

这里用到一个理论称为“牛顿-拉弗森方法（Newton-Raphson method）”,它是牛顿在 17 世纪提出的一种在实数域和复数域上近似求解方程的方法。

多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。牛顿迭代法使用函数的泰勒级数的前面几项来寻找方程的根。

求解过程

我们设方程函数 $f (x) = m$ ,改方程可以转化为 $g (x) = f (x) - m$ 我们只需要求出函数 $g (x) = 0$ 的解，就可以求出 $f (x) = m$ 的解。

牛顿迭代公式

设 $r$ 是 $f (x) = 0$ 的根，选取 $x_{0}$ 作为 $r$ 的初始近似值，则我们可以过点 $(x_{0}, f (x_{0}))$ 做曲线 $y = f (x)$ 的切线 $L$ ,我们知道切线与 $x$ 轴有交点，我们已知切线 $L$ 的方程为 $L : y = f (x_{0}) + f^{'} (x_{0}) (x - x_{0})$ 我们求的它与 $x$ 轴的交点为 $x_{1} = x_{0} - \frac{f ( x _{0} )}{f ^{'} ( x _{0} )}$ . 我们在以 $(x_{1}, f (x_{1}))$ 斜率为 $f^{'} (x_{1})$ 做斜线，求出与 $x$ 轴的交点，重复以上过程直到 $f (x_{n})$ 无限接近于 0 即可。其中第 n 次的迭代公式为：

$x_{n + 1} = x_{n} - \frac{f ( x _{n} )}{f ^{'} ( x _{n} )}$

过程理解

牛顿迭代公式可以有两种理解方法：

切线

前提：f(x)二阶可导

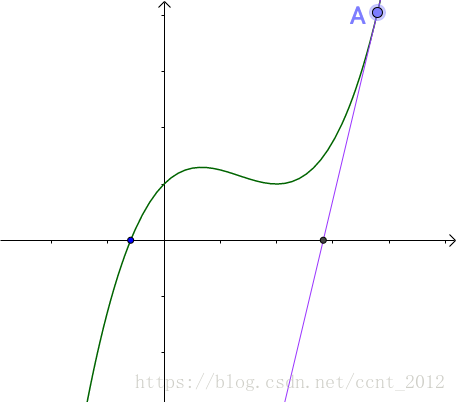
牛顿发现随便找一个曲线上的 A 点（为什么随便找，根据切线是切点附近的曲线的近似，应该在根点附近找，但是很显然我们现在还不知道根点在哪里），做一个切线，切线的根（就是和 x 轴的交点）与曲线的根，还有一定的距离。牛顿、拉弗森们想，没关系，我们从这个切线的根出发，做一根垂线，和曲线相交于 B 点，继续重复刚才的工作：

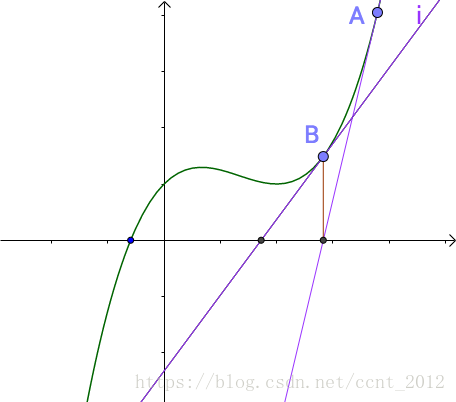
B 点比之前 A 点更接近曲线的根点，牛顿、拉弗森们很兴奋，继续重复刚才的工作：

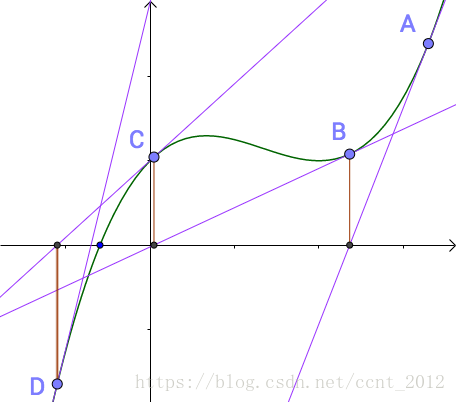
经过多次迭代后会越来越接近曲线的根（下图进行了 50 次迭代，哪怕经过无数次迭代也只会更接近曲线的根，用数学术语来说就是，迭代收敛了）：

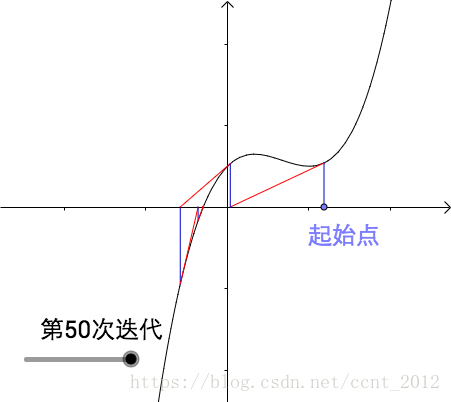
计算过程：

曲线方程 $f (x) = x^{2} - m$ ，随机取一点 $x_{1}$
$x_{1}$ 处切线方程： $y - f (x_{1}) = f^{'} (x_{1}) (x - x_{1})$ ，此方程与 x 轴交点为 $x_{2}$
$x_{2} = x_{1} - \frac{f ( x _{1} )}{f ^{'} ( x _{1} )} = x_{1} - \frac{x _{1}^{2} - m}{2 x _{1}}$
反复迭代，直到 $x_{n + 1} = x_{n} - \frac{x _{n}^{2} - m}{2 x _{n}}$ 在设定精度值满足要求情况下， $x_{n + 1}$ 即为所求的近似平方根值。

泰勒公式

$f (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) + \frac{f ^{''} ( x _{0} )}{2 !} (x - x_{0})^{2} + \dots + \frac{f ^{(n)} ( x _{0}}{n !} (x - x_{0})^{n} + R_{n} (x) $

可知，求平方根代入公式得

$f (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) + 0 + 0 + ...$

进行 n 次迭代后 $x_{n + 1} = x_{n} - \frac{f ( x )}{f ^{'} ( x )} = x_{n} - \frac{x _{n}^{2} - m}{2 x _{n}}$

当 $R_{n} (x)$ 满足精度时， $x_{n + 1}$ 即为所求的近似值。

Math.sqrt() 的代码实现

const precision = 0.00001; // 数据精度
const next = (x, n) => (x + n / x) / 2;
const sqrt = (n, precision) => {
  let x = n;
  while (Math.abs(Math.pow(x, 2) - n) > precision) {
    x = next(x, n);
  }
  return x;
};
// test
console.log(sqrt(2, precision)); // 1.4142156862745097

推广至 N 次根号 (n 阶导数)

平方根 $f (x) = x^{2} - m$

$x_{n + 1} = x_{n} - \frac{f ( x )}{f ^{'} ( x )} = x_{n} - \frac{x _{n}^{2} - m}{2 x _{n}} = \frac{1}{2} x_{n} + \frac{m}{2 x _{n}}$

立方根 $f (x) = x^{3} - m$

$x_{n + 1} = x_{n} - \frac{f ( x )}{f ^{'} ( x )} = x_{n} - \frac{x _{n}^{3} - m}{3 x _{n}^{2}} = \frac{2}{3} x_{n} + \frac{m}{3 x _{n}^{2}}$

k 次方根 $f (x) = x^{k} - m$

$x_{n + 1} = x_{n} - \frac{f ( x )}{f ^{'} ( x )} = x_{n} - \frac{x _{n}^{k} - m}{k x _{n}^{k - 1}} = \frac{k - 1}{k} x_{n} + \frac{m}{k x _{n}^{k - 1}}$

N 次根号的代码实现

const precision = 0.00001; // 数据精度
/**
 * @function
 * @description 计算下一次近似估值
 * @param x {Number} 函数自变量
 * @param k {Number} k次根值
 * @param n {Number} 初值
 * @return cur {Number}
 */
const next = (x, k, n) => ((k - 1) * x + n / Math.pow(x, k - 1)) / k;
/**
 * @function
 * @description 计算k次根值
 * @param x {Number} 函数自变量
 * @param k {Number} k次根值
 * @param precision {Number} 计算精度，可选。默认 0.00001
 * @return cur {Number}
 */
const sqrtN = (x, k, precision = 0.00001) => {
  let n = x;
  let cur = x;
  while (Math.abs(Math.pow(cur, k) - x) > precision) {
    cur = next(cur, k, n);
    console.log(
      "当前值：",
      cur,
      " 当前误差值: ",
      Math.abs(Math.pow(cur, k) - x)
    );
  }
  return cur;
};
// test
console.log(sqrtN(2, 2, precision)); // 1.4142156862745097
console.log(sqrtN(3, 2, precision)); // 1.7320508100147274
console.log(sqrtN(3, 3, precision)); // 1.4422496346010913

类似参考：